Computational Complexity

We are a research group in theoretical computer science, in particular complexity theory. Our goal is to understand which problems are easy and which problems are hard to compute. We mainly work in algebraic models, proving lower bounds for algebraic circuits as well as designing efficient algebraic algorithms.

Geometric complexity theory is an approach towards proving lower bounds in algebraic complexity theory via methods from algebraic geometry and representation theory. It was introduced by Mulmuley and Sohoni and has gained significant momentum over the last few years. The classical conjecture of Valiant that the permanent cannot be written as a projection of a polynomial-sized determinant is translated to a question of orbit closures. A number of interesting new challenges arise: Understanding the algebraic closure of traditional algebraic complexity classes, understanding nontrivial equations of the closures, and finally proving that the equations does not vanish on a given presumably hard polynomial. Christian Ikenmeyer and Markus Bläser wrote an introduction to geometric complexity theory, that addresses in particular students and scientists with a computer science background.

The field of fast matrix multiplication started when in 1969, Strassen found a way to multiply two matrices with O(n^2.81) operations. Since then, an astonishing development has taken place
yielding clever and involved constructions to resulted in asymptotically faster and faster algorithms. The current world record is O(n^2.373). While we know some (unfortunately very modest) lower bounds for the number of operations, we do not know any nontrivial lower bound on the exponent. One aim of our research is to understand the exponent of matrix multiplication better. Read more about the theory of fast matrix multiplication algorithms here >>>.

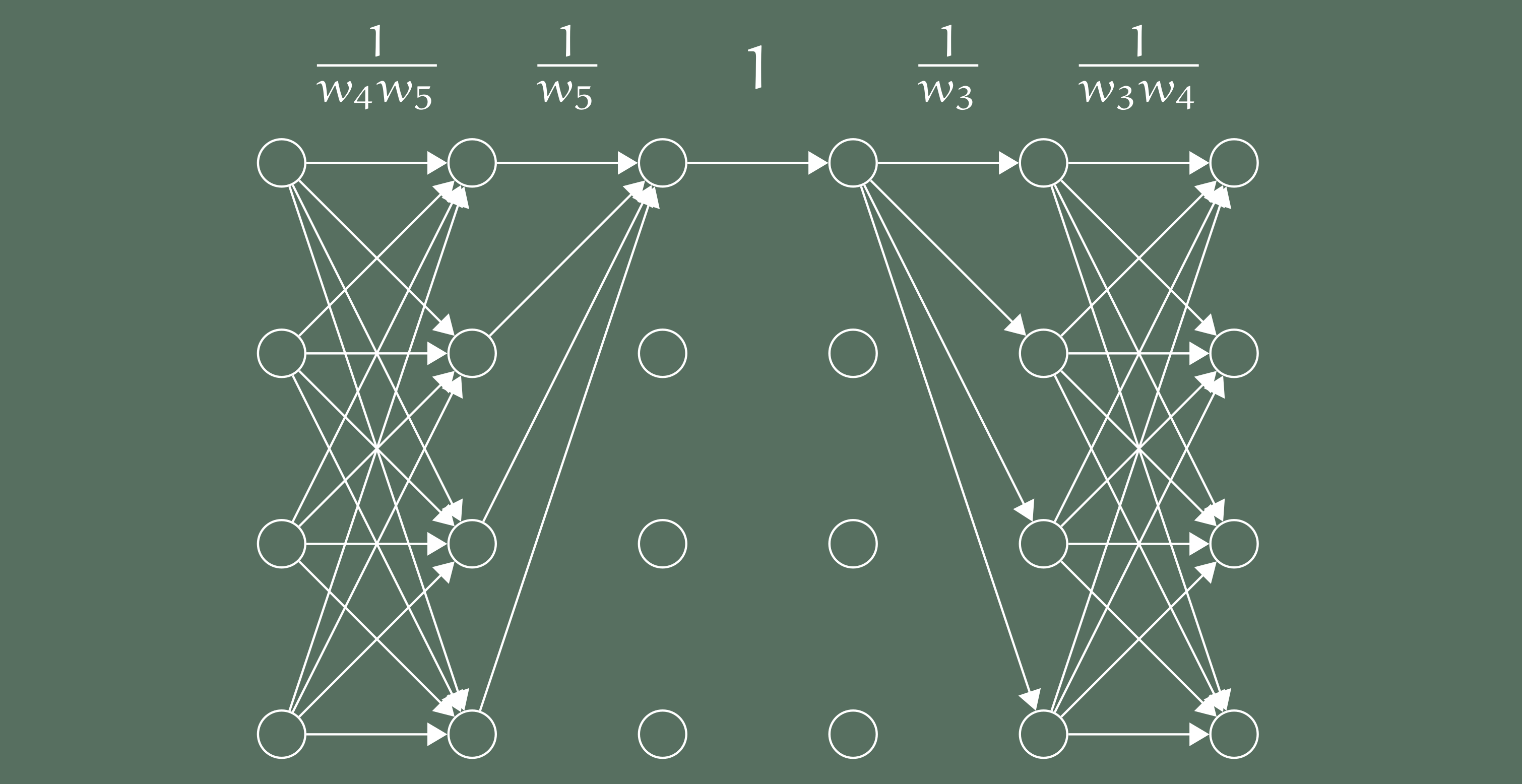
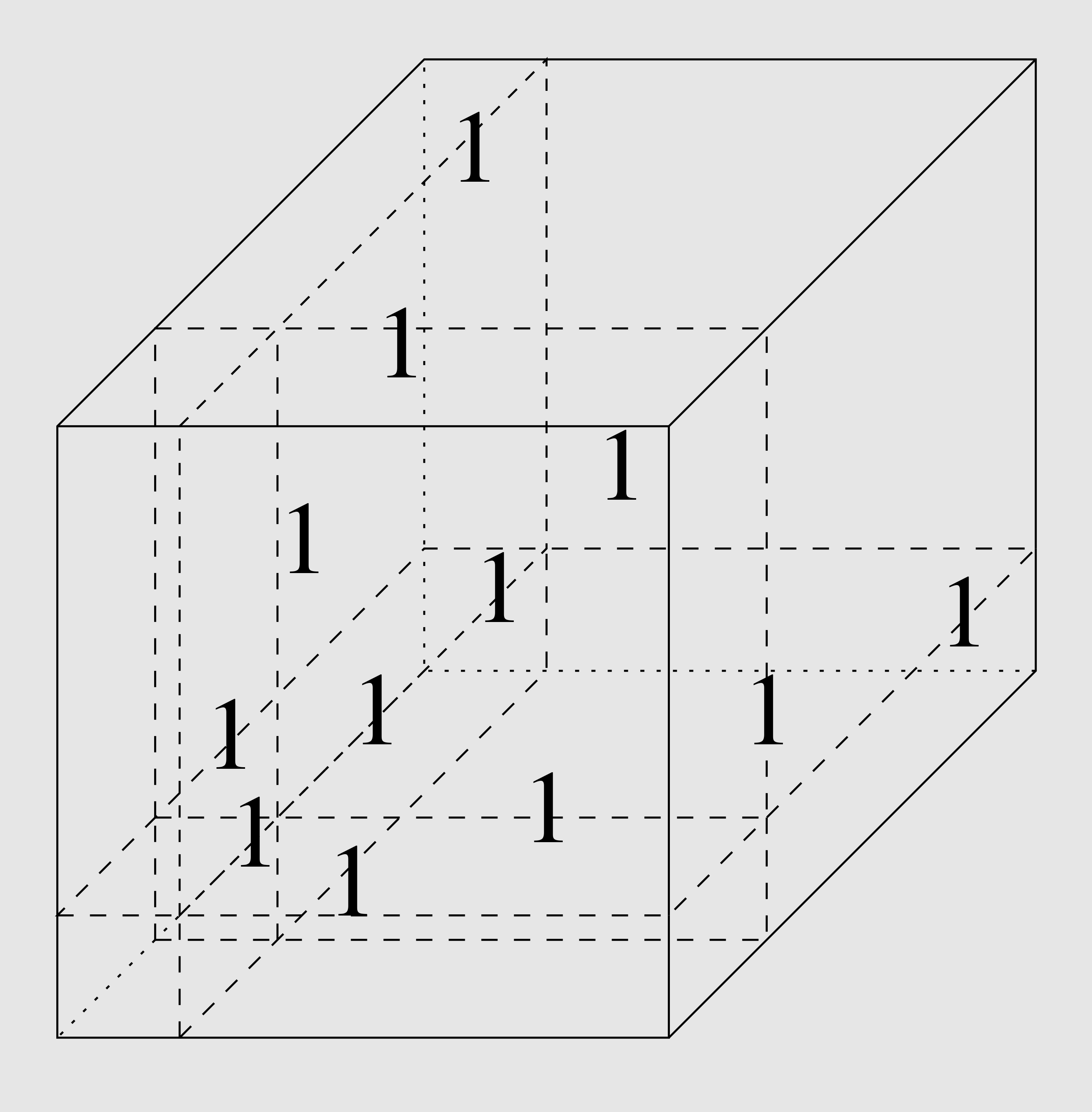
We matrix multiplication (and in general any bilinear map), we can associate a “three-dimensional” matrix, a so-called tensor. And with a tensor, we can associate a notion of rank, like with a matrix. The question about the exponent can be phrased as a tensor rank problem. The tensor rank problem provides a link to geometric complexity theory. The tensor of a certain rank are not a closed set, so we want to understand their closure, the set of tensors of minimal border rank. And the question whether a certain tensor has a certain border rank can be phrased as an orbit closure problem, so we can start applying methods from geometric complexity theory.